
Comment la valeur du cosinus peut transformer votre compréhension des angles
Dans le monde des mathématiques, la trigonométrie se déploie comme un outil essentiel pour explorer les relations angulaires et les dimensions géométriques. Au cœur de cette discipline fascinante, la valeur du cosinus émerge comme un concept clé qui anime la compréhension des angles. En décomposant ce que signifie réellement le cosinus d’un angle, nous découvrons non seulement les fondements théoriques de cette valeur, mais également des applications concrètes qui peuvent révolutionner notre approche face à des problèmes complexes.
Trigonométrie : définition, applications et importance en vie quotidienne
La trigonométrie est une branche des mathématiques qui étudie les relations entre les longueurs des côtés et les mesures des angles des triangles, en particulier les triangles rectangles. Des découvertes anciennes ont permis le développement des fonctions trigonométriques, telles que le sinus, le cosinus et la tangente, qui sont fondamentales pour résoudre une multitude de problèmes pratiques allant de l’architecture à la physique.
La valeur du cosinus, notée cos(θ), est particulièrement importante car elle représente le rapport entre la longueur du côté adjacent à un angle et celle de l’hypoténuse dans un triangle rectangle. En d’autres termes, pour un angle θ, cos(θ) = côté adjacent / hypothénuse. Cet outil, intrinsèquement lié à la notion d’angles, est omniprésent dans diverses applications de la vie quotidienne.
Dans le domaine de l’architecture, par exemple, les architectes utilisent le cosinus pour concevoir des structures complexes, en s’assurant que les angles sont précis et fonctionnels. De même, en ingénierie, le cosinus est utilisé pour analyser les forces en jeu dans diverses constructions, telles que les ponts et les bâtiments. Mais comment ces concepts trigonométriques se traduisent-ils dans des situations concrètes ?
- Modélisation de phénomènes naturels : le cosinus joue un rôle crucial dans la description de mouvements périodiques, comme les vagues ou les oscillations sonores.
- Navigation : dans l’aviation et la navigation maritime, les commandes de vol ainsi que les trajectories sont souvent calculées en utilisant des fonctions trigonométriques.
- Électromagnétisme : les courants alternatifs dans l’électricité utilisent des fonctions trigonométriques pour modéliser la distribution et les interactions d’énergie.
Ces exemples démontrent que la trigonométrie, et la valeur du cosinus en particulier, ne se limitent pas à des applications théoriques. Elles envahissent notre quotidien, facilitant la conception et la compréhension des formes et des structures que nous côtoyons tous les jours.
Pourquoi la valeur du cosinus est essentielle en trigonométrie
Pour apprécier l’importance de la valeur du cosinus, il est crucial de comprendre son origine mathématique et son interprétation géométrique. Lorsqu’un angle est tracé à partir de l’axe des abscisses dans le sens antihoraire, la valeur du cosinus donne la projection de ce point sur l’axe des x, ce qui est essentiel pour de nombreuses analyses et calculs.
Plus encore, la valeur du cosinus se lie à des concepts fondamentaux tels que la symétrie et la périodicité. Par exemple, le fait que cos(θ) = cos(-θ) illustre la symétrie par rapport à l’axe des y sur le graphique du cosinus. Cette propriété est particulièrement bénéfique lors de la résolution d’équations trigonométriques.
Utilisations en géométrie et en mathématiques
La valeur du cosinus se retrouve dans de nombreuses identités mathématiques et géométriques. L’identité fondamentale, sin²(θ) + cos²(θ) = 1, permet aux mathématiciens de résoudre des triangles éloignés et de développer des calculs plus complexes. De plus, cette identité se trouve au cœur de la loi des cosinus, qui est utilisée pour déterminer les longueurs ou les angles d’un triangle.
Voici une brève illustration de la loi des cosinus :
| Condition | Loi des Cosinus |
|---|---|
| Triangle quelconque | c² = a² + b² – 2ab cos(C) |
| Triangle rectangle | c² = a² + b² |
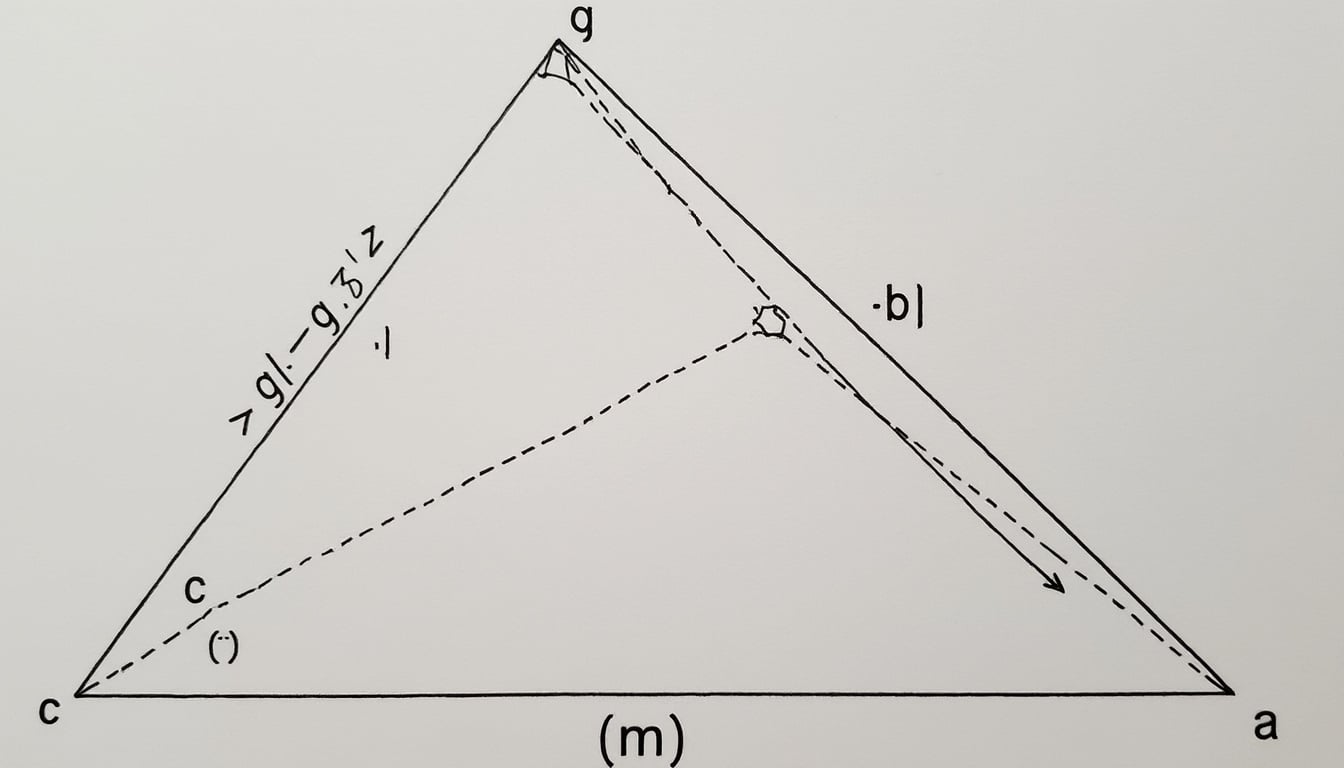
Afin d’illustrer l’importance du cosinus, prenons un exemple pratique : imaginons un architecte devant construire un toit à deux versants. Pour garantir que les angles de chaque versant sont symétriques et esthétiquement agréables, il peut s’appuyer sur le cosinus pour déterminer les longueurs précises des pentes par rapport à la ligne horizontale, optimisant à la fois l’apparence et la fonctionnalité.
Les applications pratiques de la valeur du cosinus dans la vie quotidienne
Bien que souvent perçue comme un concept théorique éloigné, la valeur du cosinus se manifeste dans de nombreux aspects concrets de notre quotidien. Qu’il s’agisse de loisirs ou de travaux professionnels, son utilisation s’étend à des domaines variés.
En arts et technologies
Dans le domaine artistique, le cosinus trouve son application dans des techniques telles que la création d’animations numériques. Les graphistes utilisent des fonctions trigonométriques pour créer des mouvements fluides et réalistes dans des vidéos et des jeux, prenant en compte la projection des mouvements de personnages sur un écran.
- Création d’animations : la projection cosinus permet de modéliser des trajectoires.
- Éclairage : la direction de la lumière sur des surfaces peut être calculée par le biais du cosinus.
Sur le terrain sportif
Dans le sport, la valeur du cosinus entre également en jeu. Prenons l’exemple d’un joueur de basket-ball qui doit évaluer l’angle optimal de tir. En utilisant les principes trigonométriques, il peut prévoir sa trajectoire et maximiser ses chances de marquer.
La relation entre la distance au panier et l’angle de lancer peut être exprimée par la formule :
Distance = 2 * hauteur * cos(θ)
Explorer les différentes méthodes pour calculer la valeur du cosinus
Calculer la valeur du cosinus demande une certaine approche stratégique, avec plusieurs méthodes disponibles qui s’adaptent selon le contexte d’utilisation.
Utilisation de calculatrices trigonométriques
Dans un cadre académique, les étudiants se tournent souvent vers des calculatrices scientifiques qui intègrent des fonctions trigonométriques. Ces outils sont essentiels pour effectuer des calculs rapides et précis, notamment lors d’examens ou de calculs complexes.
Approches géométriques et tables trigonométriques
Avant l’ère numérique, les mathématiciens utilisaient des tables trigonométriques. Grâce à ces tables, qui listent les valeurs de cosinus pour divers angles, on pouvait déterminer rapidement les valeurs souhaitées. Cette méthode impose un certain apprentissage, mais constitue une bonne alternative pour les calculs manuels.
Pour illustrer les valeurs de cosinus des angles remarquables, voici un tableau :
| Angle en degrés | Cosinus |
|---|---|
| 0° | 1 |
| 30° | √3/2 |
| 45° | √2/2 |
| 60° | 1/2 |
Comprendre (Enfin!) Cosinus et Sinus – La Baguette Math Et Magique
Pour déconstruire et appréhender ces concepts de manière efficace, l’apprentissage des relations entre le cosinus et le sinus est essentiel. Beaucoup se retrouvent intimement liés sur le cercle trigonométrique, permettant ainsi de déduire des informations sur l’un lorsque l’autre est connu.
La maîtrise des rapports trigonométriques offre une compréhension plus approfondie des phénomènes cycliques. En utilisant le cercle trigonométrique, on peut illustrer que les valeurs de cosinus et sinus sont respectivement les abscisses et ordonnées d’un point sur le cercle de rayon unité. Considérer cet aspect spatial apporte une dimension supplémentaire à notre compréhension.
FAQ
Qu’est-ce que le cosinus et son utilité ?
Le cosinus d’un angle représente le rapport entre la longueur du côté adjacent et la longueur de l’hypoténuse dans un triangle rectangle, étant essentiel pour divers calculs trigonométriques.
Comment calculer rapidement le cosinus d’un angle ?
Il existe plusieurs méthodes pour calculer le cosinus, allant de l’utilisation d’une calculatrice à la consultation de tables trigonométriques pour les valeurs des angles remarquables.
Dans quel domaine le cosinus est-il le plus utilisé ?
Le cosinus est largement utilisé dans des domaines allant de l’architecture à la navigation, en passant par l’électromagnétisme et l’animation numérique.
Quels sont les angles remarquables à retenir ?
Les angles de 30°, 45° et 60° sont les plus courants, chaque angle ayant une valeur fixe de cosinus bien connue.
Comment le cosinus est-il applicable dans le sport ?
Dans le sport, le cosinus est utilisé par les athlètes pour déterminer l’angle optimal de tir ou de lancer en maximisant leurs chances de réussite.






